Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Dietlind Bäro
Daniel Metzsch | www.matheraum.de
Mathe für's ABI 2009
Aufgabenblatt 1
Abgabe: So 01.02.2009 15:00 | 04.01.2009 | | Aufgabe 1 | Gegeben sei die Funktion f durch 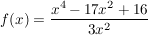
1. Bestimmen Sie den maximalen Definitionsbereich, das Symmetrieverhalten, Nullstellen (mit Steigung in den Nullstellen) und Extrempunkte sowie die Näherungsfunktion a(x) für betragsmäßig große x.
Zeichnen Sie die Graphen von f und a in dasselbe Koordinatensystem über dem Intervall [-5;5].
Die 2. Ableitung der Funktion lautet: 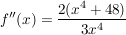
2. Berechnen Sie den Inhalt der Fläche, die vom Graphen von f und der x-Achse umschlossen wird.
3. Die Graphen von f und a umschließen zwischen der rechten Minimalstelle 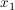 von f und der größten Nullstelle von f und der größten Nullstelle  von f eine Fläche von f eine Fläche 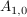 . .
Berechnen Sie diese Fläche.
Bestimmen Sie den prozentualen Anteil dieser Fläche an der ins Unendliche reichenden Fläche zwischen den beiden Graphen über dem Intervall 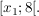
4. Betrachten Sie einen Punkt P(u;v) auf dem Graphen von f mit 1< u <4.
Die Parallele zur x-Achse durch P, die y-Achse und die Verbindungsstrecke von P zum tiefsten Punkt der Näherungsfunktion a(x) bilden ein Dreieck.
Weisen Sie nach, dass es unter diesen Dreiecken eines gibt, das den kleinsten Flächeninhalt besitzt. |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|

