FlächenbestimmungWie bestimme ich die Fläche unter einem Funktionsgraphen im 1. Quadranten?
Der Flächeninhalt unter der Funktion  soll über dem Intervall [a;b] durch Rechtecke approximiert werden. soll über dem Intervall [a;b] durch Rechtecke approximiert werden.
![Link auf "http://www.geogebra.at/de/upload/files/dynamische_arbeitsblaetter/lwolf/oberuntersumme/oberuntersumme.html" [link]](/images/popup.gif) dynamische Veranschaulichung: bitte dynamische Veranschaulichung: bitte 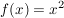 von Hand eingeben. von Hand eingeben.
Sei dazu n die Anzahl der Rechtecke, b die Ober-, a die Untergrenze.
Für Rechtecke gleicher Breite hat jedes Rechteck die Breite  . .
Die Höhe der Rechteckes berechnet sich über 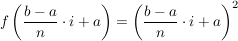 , ,
wobei i mit  die Nummer des jeweiligen Rechteckes ist. die Nummer des jeweiligen Rechteckes ist.
Folglich beträgt der Flächeninhalt des i-ten Rechteckes 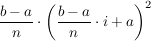 . .
Summieren wir über alle Rechtecke, erhalten wir eine Annäherung an den exakten Flächeninhalt unter der Kurve:

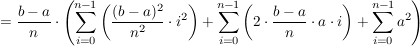
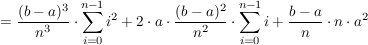
Wegen 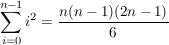 und und  (Beweis durch Induktion) folgt (Beweis durch Induktion) folgt
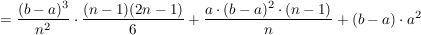
Diesen Term kann man noch weiter vereinfachen.
Will man nun den exakten Flächeninhalt berechnen, muss man die Anzahl der Rechtecke gegen unendlich gehen lassen. Dadurch werden die Rechtecke beliebig schmal. Dann ergibt sich:
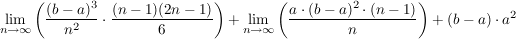
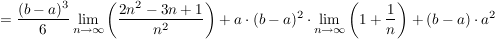
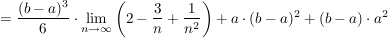
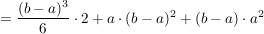
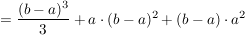
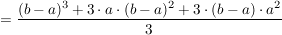
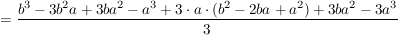

 . .
| 
