Henderson-Hasselbalch-Gleichung
Herleitung
Zur Beschreibung des pH-Wertes kann die Henderson-Hasselbalch-Gleichung herangezogen werden. Entsprechend der folgenden Säure-Base-Reaktion wird das Massenwirkungsgesetz aufgestellt. Dabei wird die Konzentration eines Stoffes immer in eckigen Klammern angegeben.
In wässrigen Systemen ist ![$ [H_2O]\approx $ $ [H_2O]\approx $](/teximg/1/7/01441071.png) konstant. Daher kann die Konzentration von Wasser auch mit in die Gleichgewichtskonstante einbezogen werden. konstant. Daher kann die Konzentration von Wasser auch mit in die Gleichgewichtskonstante einbezogen werden.
Durch einfaches Umstellen erhält man
Durch Logarithmieren erhält man
Der ganze Term wird mit -1 multipliziert.
Nun kann durch den pH- und den 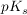 -Wert substituiert werden. -Wert substituiert werden.
oder auch
Bedeutung am Halbäquivalenzpunkt
Wird beispielsweise Essigsauere mit Natronlauge titriert, so kann der 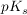 -Wert der Essigsauere ermittelt werden. Am Halbäquivalenzpunkt gilt -Wert der Essigsauere ermittelt werden. Am Halbäquivalenzpunkt gilt ![$ [HA]=[A^-] $ $ [HA]=[A^-] $](/teximg/9/6/01441069.png) und für die Gleichung erhält man und für die Gleichung erhält man
Verdünnen von Pufferlösungen
Beim Verdünnen von Pufferlösungen bleibt der 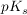 -Wert logischerweise konstant. Da sowohl [HA] wie auch -Wert logischerweise konstant. Da sowohl [HA] wie auch ![$ [A^-] $ $ [A^-] $](/teximg/0/7/01441070.png) beim Verdünnen im gleichen Masse kleiner werden bleibt auch der pH-Wert konstant. beim Verdünnen im gleichen Masse kleiner werden bleibt auch der pH-Wert konstant.
| 
