IntervallschachtelungDefinition Intervallschachtelung
Schule
Eine Folge von Intervallen bildet eine Intervallschachtelung, wenn
- jedes Intervall im vohergehenden enthalten ist und
- die Intervall-Längen abnehmen und beliebig klein werden.
Jede Intervallschachtelung bestimmt auf der Zahlengeraden genau einen Punkt, d.h. genau eine Zahl.
Beispiel:
Wie kann man 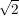 immer genauer berechnen? immer genauer berechnen?
Man kann das zwar einfach in einen Taschenrechner eintippen, und der weiß das Ergebnis, aber man hat keine Ahnung, wie man selber drauf kommt.
Also das einzige, was man genau von 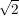 weiß, ist weiß, ist 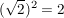 . .
Und jetzt geht man wie bei dem Raten "heiss...kalt" vor. Man probiert 1,5 und stellt fest:
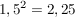 ist zu groß; also kleiner ist zu groß; also kleiner 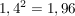 ist zu klein; also zwischen 1,4 und 1,5 liegt das gesuchte. ist zu klein; also zwischen 1,4 und 1,5 liegt das gesuchte.
Man schreibt:
Alle Zahlen zwischen 1,4 und 1,5 sind das Intervall, das 0,1 Einheiten lang ist. Jetzt will man's genauer wissen und probiert 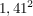 zu klein, zu klein, 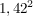 zu groß: also hat man ein kleineres Intervall, nur noch 0,01 lang: zu groß: also hat man ein kleineres Intervall, nur noch 0,01 lang:
Jetzt 1,411; 1,412; 1,413 1,414 Quadrate alle kleiner als 2; dann 1,415 Quadrat größer 2, also weiß man jetzt
und muss nur noch bei Zahlen zwischen den beiden suchen.
Also haben wir die gesuchte Zahl weiter eingeengt. Das Intervall ist nur noch 0,0001 lang.
Alle diese Intervalle liegen ineinander, im innersten, in dem man grade angekommen ist, liegt immer noch ein kleineres.
So, und jetzt stecken die Intervalle ineinander, wie immer kleinere Schachteln ineinander liegen. Deshalb nennt man das Intervallschachtelung.
Universität
| 
