LagrangeSatz von Lagrange
Sei G eine endliche Gruppe und 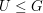 . Dann gilt: . Dann gilt:
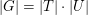
mit T Links- oder Rechtstransversale von U in G. Insbesondere haben alle Transversalen von U in G gleiche Mächtigkeit.
Diese Anzahl heißt Index von U in G, schreibe |G:U|. Also gilt:
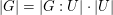 . .
Beweis
T Linkstransversale von U in G 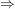 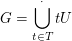 und und 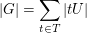 . .
Wegen |tU|=|U| folgt:
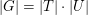 , ,
denn 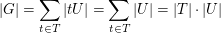 . . 
Korollar (Kleiner Satz von Fermat)
Sei 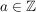 nicht durch eine Primzahl p teilbar. Dann gilt: nicht durch eine Primzahl p teilbar. Dann gilt: 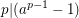 . .
(Beweis: Die Gruppe der invertierbaren Elemente in 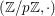 hat Ordnung p-1.) hat Ordnung p-1.)
Verallgemeinerung des Satzes
Sind U und V Untergruppen der endlichen Gruppe G mit 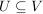 , dann gilt , dann gilt
![$ [G : U] = [G : V ] \cdot [V : U] $ $ [G : U] = [G : V ] \cdot [V : U] $](/teximg/8/3/02449538.png) . .
Beweis
Wende den Satz von Lagrange mehrfach an und kürze |U| heraus:
![$ |G| = [G:U] \cdot |U| = [G:V] \cdot |V| = [G:V ] \cdot [V:U]\cdot|U| $ $ |G| = [G:U] \cdot |U| = [G:V] \cdot |V| = [G:V ] \cdot [V:U]\cdot|U| $](/teximg/9/3/02449539.png) . . 
Anwendung
Sei 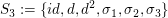 die symmetrische Gruppe, wobei die symmetrische Gruppe, wobei
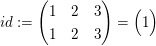 , , 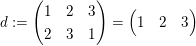 , , 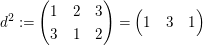 , ,
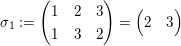 , , 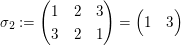 , , 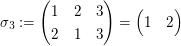 . .
Es ist ord(id)=1, 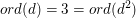 und und 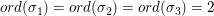 . .
Wir bestimmen nun alle Untergruppen von 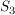 . .
Wegen 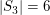 hat hat 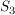 höchstens Untergruppen der Ordnung 1,2,3 und 6. Die trivialen Untergruppen höchstens Untergruppen der Ordnung 1,2,3 und 6. Die trivialen Untergruppen 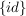 bzw. bzw. 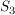 haben Ordnung 1 bzw. 6 und sind einzige Untergruppen dieser Ordnungen. haben Ordnung 1 bzw. 6 und sind einzige Untergruppen dieser Ordnungen.
Elemente der Ordung 2 erzeugen folgende zweielementige Untergruppen, die die einzigen Untergruppen mit Ordung 2 sind:
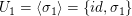 , , 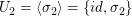 und und 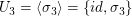
Wegen 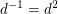 ist ist 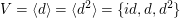 . Zudem ist V einzige Untergruppe mit Ordnung 3. Denn jede andere Untergruppe mit drei Elementen enthält ein . Zudem ist V einzige Untergruppe mit Ordnung 3. Denn jede andere Untergruppe mit drei Elementen enthält ein 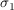 , , 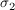 oder oder 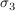 und ist deshalb Untergruppe der Ordung 2. Nach Lagrange hat sie dann nicht Ordnung 3. und ist deshalb Untergruppe der Ordung 2. Nach Lagrange hat sie dann nicht Ordnung 3.
Literatur
isbn9783827430113 C. Karpfinger, K. Meyberg: Algebra, Springer Spektrum, 2013
| 
