www.matheraum.de
Das Matheforum.
Das Matheforum des MatheRaum.

Für Schüler, Studenten, Lehrer, Mathematik-Interessierte.
Hallo Gast! [ einloggen | registrieren ]
Startseite · Forum · Wissen · Kurse · Mitglieder · Team · Impressum
Forenbaum
^ Forenbaum
Status Mathe
  Status Schulmathe
    Status Primarstufe
    Status Mathe Klassen 5-7
    Status Mathe Klassen 8-10
    Status Oberstufenmathe
    Status Mathe-Wettbewerbe
    Status Sonstiges
  Status Hochschulmathe
    Status Uni-Analysis
    Status Uni-Lin. Algebra
    Status Algebra+Zahlentheo.
    Status Diskrete Mathematik
    Status Fachdidaktik
    Status Finanz+Versicherung
    Status Logik+Mengenlehre
    Status Numerik
    Status Uni-Stochastik
    Status Topologie+Geometrie
    Status Uni-Sonstiges
  Status Mathe-Vorkurse
    Status Organisatorisches
    Status Schule
    Status Universität
  Status Mathe-Software
    Status Derive
    Status DynaGeo
    Status FunkyPlot
    Status GeoGebra
    Status LaTeX
    Status Maple
    Status MathCad
    Status Mathematica
    Status Matlab
    Status Maxima
    Status MuPad
    Status Taschenrechner

Gezeigt werden alle Foren bis zur Tiefe 2

Navigation
 Startseite...
 Neuerdings beta neu
 Forum...
 vorwissen
   Einstieg
   
   Index aller Artikel
   
   Hilfe / Dokumentation
   Richtlinien
   Textgestaltung
 vorkurse...
 Werkzeuge...
 Nachhilfevermittlung beta...
 Online-Spiele beta
 Suchen
 Verein...
 Impressum
Das Projekt
Server und Internetanbindung werden durch Spenden finanziert.
Organisiert wird das Projekt von unserem Koordinatorenteam.
Hunderte Mitglieder helfen ehrenamtlich in unseren moderierten Foren.
Anbieter der Seite ist der gemeinnützige Verein "Vorhilfe.de e.V.".
Partnerseiten
Mathe-Seiten:Weitere Fächer:

Open Source FunktionenplotterFunkyPlot: Kostenloser und quelloffener Funktionenplotter für Linux und andere Betriebssysteme
Startseite > Orthogonalisierungsverfahren
Foren für weitere Schulfächer findest Du auf www.vorhilfe.de z.B. Informatik • Physik • Technik • Biologie • Chemie
Orthogonalisierungsverfahren
Mach mit! und verbessere/erweitere diesen Artikel!
Artikel • Seite bearbeiten • Versionen/Autoren

Orthogonalisierungsverfahren

Orthogonalisierung zum Lösen linearer Gleichungssysteme


Beschreibung

Man möchte ein Gleichungssystem Ax=b lösen. Dazu berechnet man eine Zerlegung der Matrix A in das Produkt zweier Matrizen A=QR. Wobei diese Matrizen folgende schöne Eigenschaften haben:

$ Q^T=Q^{-1} $

$ R=\pmat{r_{11} & \cdots & r_{1n} \\ \vdots & \ddots &\vdots &\\ 0 & \cdots & r_{nn}} $

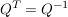
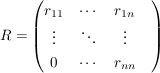
Die Inverse von Q ist also gleich ihrer Transponierten und R ist eine obere Dreiecksmatrix. Deren Lösung man durch Rückwärtseinsetzen bestimmen kann.


Algorithmus

Gegeben (A,b)
Gesucht die Lösung x von Ax=b

1. Berechne die QR-Zerlegung von A
       A->(Q,R)

2. Berechne 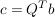$ c=Q^Tb $

3. Löse das Dreieckssystem Rx=c


Verfahren zur praktischen Umsetzung

Householder Spiegelungen

Givens Drehungen

Gram-Schmidt Orthogonalisierung


Matheraum Links




Fragen zum Artikel

Fragen zu diesem Artikel können im [link]Matheforum gestellt werden.

Erstellt: Fr 25.02.2005 von mathemaduenn
Letzte Änderung: Mo 18.09.2006 um 09:03 von mathemaduenn
Artikel • Seite bearbeiten • Versionen/Autoren • Titel ändern • Artikel löschen • Quelltext
^ Seitenanfang ^
www.matheforum.net
[ Startseite | Forum | Wissen | Kurse | Mitglieder | Team | Impressum ]