PotenzgesetzPotenzgesetze
Schule
Sofern die einzelnen Potenzen definiert sind, gelten folgende Rechengesetze:
P1)
a) 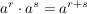
"Potenzen mit gleicher Basis werden multipliziert, indem man die Exponenten addiert und die Basis beibehält."
b) 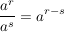
"Potenzen mit gleicher Basis werden dividiert, indem man die Exponenten subtrahiert und die Basis beibehält."
P2)
a) 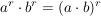
"Potenzen mit gleichem Exponenten werden multipliziert, indem man das Produkt der beiden Basiszahlen mit dem gemeinsamen Exponenten potenziert."
b) 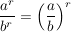
"Potenzen mit gleichem Exponenten werden dividiert, indem man den Quotienten der beiden Basiszahlen mit dem gemeinsamen Exponenten potenziert."
P3)
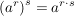
"Eine Potenz wird potenziert, indem man die Exponenten multipliziert."
weitere Identitäten, die sofort aus der Definition einer Potenz folgen:
Ausserdem sind folgende Potenzen definiert:
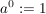 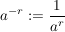 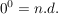 undefiniert, in manchen Zusammenhängen ist aber die Festlegung undefiniert, in manchen Zusammenhängen ist aber die Festlegung 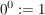 sinnvoll (da sinnvoll (da 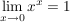 ) )
Bemerkungen.
Da Wurzeln nichts anderes sind als Potenzen mit gebrochenen Exponenten, gelten auch für Wurzelterme dieselben Regeln.
![$ \wurzel[m]{a}=a^{\bruch{1}{m}} $ $ \wurzel[m]{a}=a^{\bruch{1}{m}} $](/teximg/1/2/00674921.png) und und
![$ \wurzel[m]{a^n}=(a^n)^\bruch{1}{m}=a^\bruch{n}{m}=(\wurzel[m]{a})^n $ $ \wurzel[m]{a^n}=(a^n)^\bruch{1}{m}=a^\bruch{n}{m}=(\wurzel[m]{a})^n $](/teximg/6/2/00674926.png)
Beispiele.
Beweis.
Universität
Voraussetzungen und Behauptung
Bemerkungen.
Weitere Bemerkungen zum Verständnis des Satzes.
Beispiele.
Beweis.
| 
