QuotientenregelQuotientenregel.
Schule
Merkregel:
Universität
Hat eine Funktion 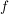 die Form die Form
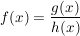 (mit (mit 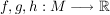 , wobei , wobei 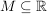 ) )
und ist  aus dem Definitionsbereich von aus dem Definitionsbereich von 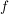 , so gilt, unter den Voraussetzungen, dass , so gilt, unter den Voraussetzungen, dass  und und 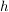 in in  differenzierbar sind und im Falle differenzierbar sind und im Falle 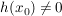 : :
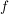 ist diff'bar in ist diff'bar in  und es gilt und es gilt
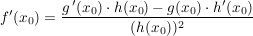
Beweis
Da 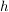 diff'bar in diff'bar in  ist, gilt insbesondere, dass ist, gilt insbesondere, dass 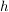 stetig in stetig in  ist. ist.
(Denn: Sei 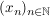 eine Folge in eine Folge in 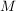 mit mit 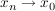 ( (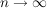 ), ), 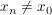 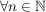 . .
Dann gilt:
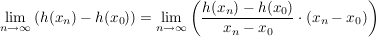
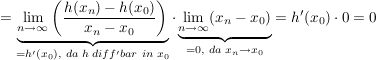 , ,
also 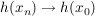 ( (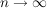 ).) ).)
Sei 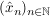 eine Folge in eine Folge in 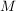 mit mit 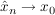 ( (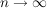 ), ),  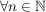 . .
Weil 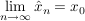 und weil und weil 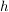 stetig in stetig in  ist, gilt insbesondere: ist, gilt insbesondere:
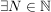 : : 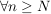 : : 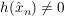 (beachte: (beachte: 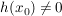 ). ).
Es folgt für alle 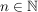 , , 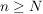 : :
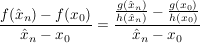
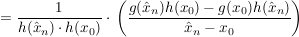
![$ =\frac{1}{h(\hat{x}_n)\cdot{}h(x_0)}\cdot{}\left(\frac{[\,g(\hat{x}_n)-g(x_0)]\cdot{}h(x_0)+g(x_0)\cdot{}h(x_0)-g(x_0)h(\hat{x}_n)}{\hat{x}_n-x_0} \right) $ $ =\frac{1}{h(\hat{x}_n)\cdot{}h(x_0)}\cdot{}\left(\frac{[\,g(\hat{x}_n)-g(x_0)]\cdot{}h(x_0)+g(x_0)\cdot{}h(x_0)-g(x_0)h(\hat{x}_n)}{\hat{x}_n-x_0} \right) $](/teximg/4/0/00386904.png)
![$ =\frac{1}{h(\hat{x}_n)\cdot{}h(x_0)}\cdot{}\left(\frac{[\,g(\hat{x}_n)-g(x_0)]\cdot{}h(x_0)-g(x_0)[\,h(\hat{x}_n)-h(x_0)]}{\hat{x}_n-x_0}\right) $ $ =\frac{1}{h(\hat{x}_n)\cdot{}h(x_0)}\cdot{}\left(\frac{[\,g(\hat{x}_n)-g(x_0)]\cdot{}h(x_0)-g(x_0)[\,h(\hat{x}_n)-h(x_0)]}{\hat{x}_n-x_0}\right) $](/teximg/5/0/00386905.png)
Weil  und und 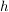 diff'bar in diff'bar in 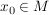 , und weil (siehe oben) , und weil (siehe oben) 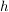 stetig in stetig in  ist, folgt: ist, folgt:

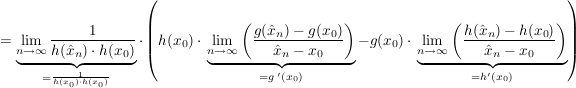
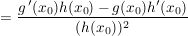
| 
