Wie man das Bild einer linearen Abbildung bestimmtGegeben sei eine lineare Abbildung 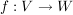 mit mit  und und  . .
Das Bild einer Abbildung ist ja die Menge aller Vektoren aus W, zu denen es ein Urbild gibt:
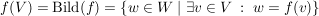
Hat man bereits eine Basis  von von 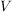 vorliegen, so wird das Bild von f von den Bildern der Basisvektoren aufgespannt: vorliegen, so wird das Bild von f von den Bildern der Basisvektoren aufgespannt:

Ist die beschreibende Matrix 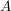 dieser linearer Abbildung bekannt (dies ist eine dieser linearer Abbildung bekannt (dies ist eine 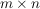 -Matrix -Matrix  (bzgl. einer geeigneten Basis), für die gilt: (bzgl. einer geeigneten Basis), für die gilt:  für alle für alle 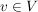 ), so ist das Bild einfach der Span der Spaltenvektoren: ), so ist das Bild einfach der Span der Spaltenvektoren:
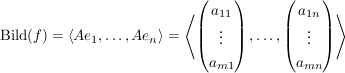
Um eine "kompaktere" Darstellung des Bildes zu erhalten, empfiehlt sich die Bestimmung einer Basis des Bildes.
Beispiele
a) Gegeben ist die Matrix 
Nach den obigen Ausführungen ist 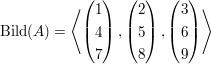 . .
Da der dritte Vektor eine Linearkombination der ersten beiden Vektoren ist, die ohnehin im Span enthalten ist, kann auf die Angabe des dritten Vektors verzeichtet werden und man erhält die kompaktere Darstellung  . Hier sind nun beide Vektoren linear unabhängig, sie bilden also eine Basis des Bildes. . Hier sind nun beide Vektoren linear unabhängig, sie bilden also eine Basis des Bildes.
| 
