Benutzer:tobit09/Beweis-Anleitung Beispiel-MengengleichheitWie führe ich einen Beweis?
 b) Teilmengenbeziehung 2 b) Teilmengenbeziehung 2  5. Beispiele 5. Beispiele 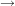 d) Gruppe d) Gruppe
5. Beispiele
c) Gleichheit von Mengen
Aufgabe:
Seien 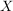 , , und und 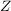 Mengen. Zeigen Sie, dass Mengen. Zeigen Sie, dass 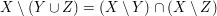 gilt. gilt.
Vorbereitung des Beweises:
Voraussetzungen:
Keine speziellen.
Behauptung:
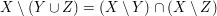
Dabei ist
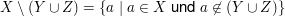 , ,
wobei
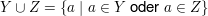 , ,
sowie
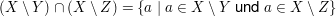 , ,
wobei
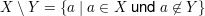
und
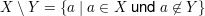 . .
Rahmen des Beweises:
Zu zeigen ist also eine Gleichheit von Mengen. Punkt h) unter 3. Wie zeige ich...? verrät uns, was zu tun ist: Wir haben nacheinander 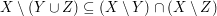 und und 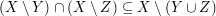 zu zeigen. zu zeigen.
Fangen wir mit 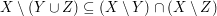 an. Punkt i) unter 3. Wie zeige ich...? verrät uns, was dazu zu tun ist: Wir betrachten ein beliebig vorgegebenes Element an. Punkt i) unter 3. Wie zeige ich...? verrät uns, was dazu zu tun ist: Wir betrachten ein beliebig vorgegebenes Element 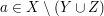 und zeigen unter der zusätzlichen Voraussetzung und zeigen unter der zusätzlichen Voraussetzung 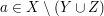 , dass auch , dass auch 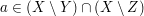 gilt. gilt.
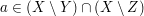 bedeutet bedeutet  und und 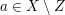 . Punkt a) unter 3. Wie zeige ich...? verrät uns, dass wir für diese "und"-Aussage nacheinander die beiden Aussagen zeigen müssen. . Punkt a) unter 3. Wie zeige ich...? verrät uns, dass wir für diese "und"-Aussage nacheinander die beiden Aussagen zeigen müssen.  bedeutet bedeutet 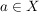 und und 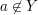 . Nacheinander sind also diese beiden Aussagen zu zeigen. . Nacheinander sind also diese beiden Aussagen zu zeigen. 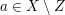 bedeutet bedeutet 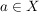 und und 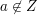 . Auch diese Aussagen sind nacheinander zu zeígen. . Auch diese Aussagen sind nacheinander zu zeígen.
Kommen wir nun zum Beweisrahmen für 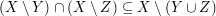 . Wir betrachten wieder wie in Punkt i) unter 3. Wie zeige ich...? beschrieben ein beliebig vorgegebenes Elemente . Wir betrachten wieder wie in Punkt i) unter 3. Wie zeige ich...? beschrieben ein beliebig vorgegebenes Elemente 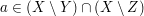 und zeigen unter der zusätzlichen Voraussetzung und zeigen unter der zusätzlichen Voraussetzung 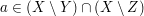 , dass auch , dass auch 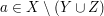 gilt. gilt.
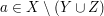 bedeutet bedeutet 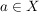 und und 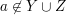 . Letzteres bedeutet "nicht . Letzteres bedeutet "nicht 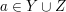 ". Punkt e) unter 3. Wie zeige ich...? verrät uns, was dazu zu tun ist: Wir nehmen ". Punkt e) unter 3. Wie zeige ich...? verrät uns, was dazu zu tun ist: Wir nehmen 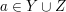 an und führen diese Annahme zu einem Widerspruch. an und führen diese Annahme zu einem Widerspruch.
Somit ergibt sich folgender Beweisrahmen:
Zu zeigen ist, dass 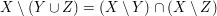 gilt. gilt.
"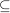 ": ":
Sei 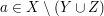 . .
Zu zeigen ist 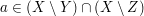 , d.h. , d.h.  und und 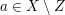 . .
...
Hauptteil für "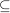 " "
( , d.h. , d.h. 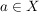 und und 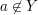 , zeigen.) , zeigen.)
(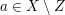 , d.h. , d.h. 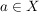 und und 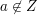 , zeigen.) , zeigen.)
...
Somit gilt 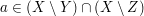 . .
Da 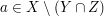 beliebig war, folgt beliebig war, folgt 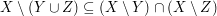 . .
"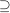 ": ":
Sei 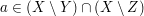 . .
Zu zeigen ist 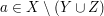 , d.h. , d.h. 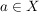 und und 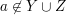 . .
...
Hauptteil für "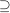 " "
(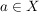 zeigen.) zeigen.)
(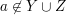 zeigen. Dazu:) zeigen. Dazu:)
Angenommen 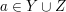 . .
(Widerspruch folgern)
...
Somit gilt 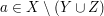 . .
Da 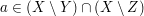 beliebig war, folgt beliebig war, folgt 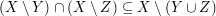 . .
Damit ist 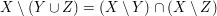 gezeigt. gezeigt.
Hauptteil des Beweises:
Fangen wir mit dem Hauptteil des Nachweises von 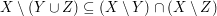 an. Wir haben als zusätzliche Voraussetzung an. Wir haben als zusätzliche Voraussetzung 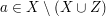 . Das bedeutet: . Das bedeutet: 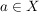 und und 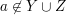 . Letzteres bedeutet (nicht . Letzteres bedeutet (nicht 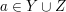 ), d.h. (nicht ( ), d.h. (nicht (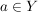 oder oder 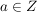 )). Punkt e) unter 4. Wie benutze ich...? verrät uns, wie wir eine solche "nicht"-Aussage verwenden können: Wir über überlegen uns, was sie in unserem Fall bedeutet, nämlich (nicht )). Punkt e) unter 4. Wie benutze ich...? verrät uns, wie wir eine solche "nicht"-Aussage verwenden können: Wir über überlegen uns, was sie in unserem Fall bedeutet, nämlich (nicht 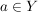 ) und (nicht ) und (nicht 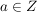 ). Punkt a) unter 4. Wie benutze ich...? verrät uns, wie wir eine solche "und"-Aussage verwenden können: Wir betrachten sowohl (nicht ). Punkt a) unter 4. Wie benutze ich...? verrät uns, wie wir eine solche "und"-Aussage verwenden können: Wir betrachten sowohl (nicht 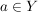 ) als auch (nicht ) als auch (nicht 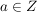 ) als zusätzliche Voraussetzungen, unter denen wir weiterargumentieren. Damit haben wir schon alle Aussagen, die wir für unsere gerade betrachtete Teilmengenbeziehung benötigen. ) als zusätzliche Voraussetzungen, unter denen wir weiterargumentieren. Damit haben wir schon alle Aussagen, die wir für unsere gerade betrachtete Teilmengenbeziehung benötigen.
Kommen wir nun zum Hauptteil des Nachweises von 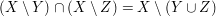 . Wir haben hier als zusätzliche Voraussetzung . Wir haben hier als zusätzliche Voraussetzung 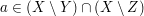 . Das bedeutet: . Das bedeutet:  und und 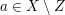 . Punkt a) unter 4. Wie benutze ich...? verrät uns wieder, wie wir eine solche "und"-Aussage verwenden können: Wir betrachten sowohl . Punkt a) unter 4. Wie benutze ich...? verrät uns wieder, wie wir eine solche "und"-Aussage verwenden können: Wir betrachten sowohl  als auch als auch 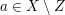 als zusätzliche Voraussetzungen, unter denen wir weiterargumentieren. als zusätzliche Voraussetzungen, unter denen wir weiterargumentieren.  bedeutet bedeutet 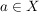 und und 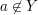 , , 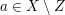 bedeutet bedeutet 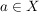 und und 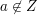 . Wir haben also als zusätzliche Voraussetzungen, unter denen wir weiterargumentieren können: . Wir haben also als zusätzliche Voraussetzungen, unter denen wir weiterargumentieren können: 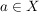 , , 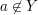 und und 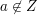 . .
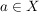 war auch zu zeigen. Außerdem ist die Annahme war auch zu zeigen. Außerdem ist die Annahme 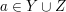 zum Widerspruch zu führen. zum Widerspruch zu führen. 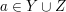 bedeutet bedeutet 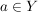 oder oder 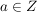 . Punkt b) unter 4. Wie benutze ich...? legt uns für diese "oder"-Aussage eine Fallunterscheidung nach . Punkt b) unter 4. Wie benutze ich...? legt uns für diese "oder"-Aussage eine Fallunterscheidung nach 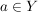 bzw. bzw. 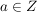 nahe. Falls nahe. Falls 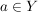 haben wir einen Widerspruch zu haben wir einen Widerspruch zu 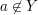 . Falls . Falls 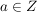 haben wir einen Widerspruch zu haben wir einen Widerspruch zu 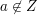 . Also haben wir in allen Fällen einen Widerspruch hergeleitet und damit . Also haben wir in allen Fällen einen Widerspruch hergeleitet und damit 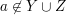 gezeigt. gezeigt.
Fertiger Beweis:
Zu zeigen ist, dass 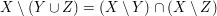 gilt. gilt.
"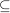 ": ":
Sei 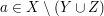 . .
Zu zeigen ist 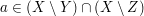 , d.h. , d.h.  und und 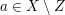 . .
Wegen 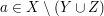 gilt gilt 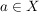 und und 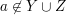 . .
Letzteres bedeutet (nicht 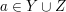 ), also (nicht ( ), also (nicht (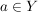 oder oder 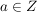 )), was (nicht )), was (nicht 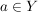 ) und (nicht ) und (nicht 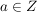 ) bedeutet, was sich wiederum als ) bedeutet, was sich wiederum als 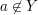 und und 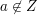 schreiben lässt. schreiben lässt.
Wegen 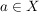 und und 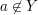 gilt gilt  . .
Wegen 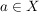 und und 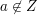 gilt gilt 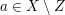 . .
Somit gilt 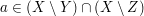 . .
Da 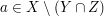 beliebig war, folgt beliebig war, folgt 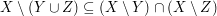 . .
"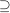 ": ":
Sei 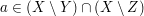 . .
Zu zeigen ist 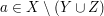 , d.h. , d.h. 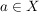 und und 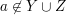 . .
Wegen 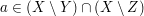 gilt gilt  und und 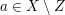 . .
 bedeutet bedeutet 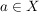 und und 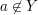 . .
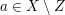 bedeutet bedeutet 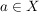 und und 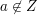 . .
Da 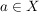 somit gezeigt ist, bleibt nur noch somit gezeigt ist, bleibt nur noch 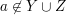 zu zeigen. zu zeigen.
Angenommen 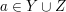 . .
Dann gilt 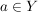 oder oder 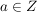 . .
Falls 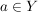 , haben wir einen Widerspruch zu , haben wir einen Widerspruch zu 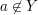 . .
Falls 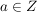 , haben wir einen Widerspruch zu , haben wir einen Widerspruch zu 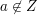 . .
Also haben wir in jedem Fall einen Widerspruch.
Also war unsere Annahme 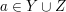 falsch und somit gilt falsch und somit gilt 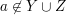 . .
Somit gilt 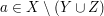 . .
Da 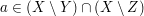 beliebig war, folgt beliebig war, folgt 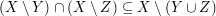 . .
Damit ist 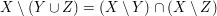 gezeigt. gezeigt.
| 
