Benutzer:tobit09/Beweis-Anleitung Zeige-AnleitungWie führe ich einen Beweis?
 2. Grundsätzliches zum Beweisen 2. Grundsätzliches zum Beweisen  Inhaltsverzeichnis Inhaltsverzeichnis  4. Wie benutze ich...? 4. Wie benutze ich...?
3. Wie zeige ich...?
a) Wie zeige ich eine "und"-Aussage?
Für eine Aussage der Form  zeige nacheinander die Aussagen zeige nacheinander die Aussagen 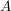 und und 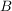 . .
Beispiele: Teilmengenbeziehung 2, Gleichheit von Mengen
b) Wie zeige ich eine "oder"-Aussage?
Für eine Aussage der Form  führe eine Fallunterscheidung nach geeigneten Aussagen führe eine Fallunterscheidung nach geeigneten Aussagen 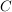 und und 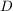 durch, für die durch, für die 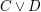 als wahr bekannt ist. Zeige, dass im Falle als wahr bekannt ist. Zeige, dass im Falle 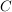 die Aussage die Aussage 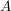 zutrifft und im Falle zutrifft und im Falle 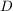 die Aussage die Aussage 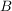 zutrifft. zutrifft.
Falls sich aus den Voraussetzungen eine Aussage der Form 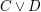 entnehmen lässt, sind diese Aussagen entnehmen lässt, sind diese Aussagen 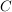 und und 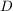 gute Kandidaten für die Fallunterscheidung. Anderenfalls kann gute Kandidaten für die Fallunterscheidung. Anderenfalls kann 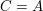 und und 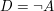 gute Dienste leisten. gute Dienste leisten.
Beispiele: Teilmengenbeziehung 1 (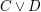 aus Voraussetzungen), Teilmengenbeziehung 2 ( aus Voraussetzungen), Teilmengenbeziehung 2 (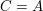 und und 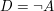 ) )
c) Wie zeige ich eine "es folgt"-Aussage?
Für eine Aussage der Form 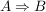 nimm nimm 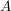 als zusätzliche Voraussetzung an ("Gelte als zusätzliche Voraussetzung an ("Gelte 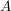 .") und zeige .") und zeige 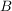 . .
Beispiel: Injektivität, Bilder und Urbilder
d) Wie zeige ich eine "genau dann, wenn"-Aussage?
Für eine Aussage der Form  zeige nacheinander zeige nacheinander 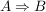 und und 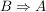 wie in c) beschrieben. wie in c) beschrieben.
Beispiel: Injektivität, Bilder und Urbilder
e) Wie zeige ich eine "nicht"-Aussage?
Für eine Aussage der Form 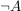 nimm nimm 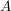 als zusätzliche Voraussetzung an ("Angenommen als zusätzliche Voraussetzung an ("Angenommen 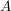 .") und führe diese Annahme zu einem Widerspruch. .") und führe diese Annahme zu einem Widerspruch.
Beispiel: Gleichheit von Mengen
f) Wie zeige ich eine "für alle"-Aussage?
Für eine Aussage der Form  betrachte ein beliebig vorgegebenes Element betrachte ein beliebig vorgegebenes Element  ("Sei ("Sei  .") und zeige unter der zusätzlichen Voraussetzung .") und zeige unter der zusätzlichen Voraussetzung  für dieses Element für dieses Element  die Aussage die Aussage  . .
Da  beliebig vorgegeben war, gilt somit beliebig vorgegeben war, gilt somit  für alle für alle  . .
Beispiele: Surjektivität, Injektivität, Bilder und Urbilder
g) Wie zeige ich eine "es existiert"-Aussage?
Für eine Aussage der Form 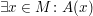 finde ein Beispiel-Element finde ein Beispiel-Element  , für das , für das  gilt. gilt.
Häufig folgt die Existenz eines  , für das sich , für das sich  zeigen lässt, aus einer Voraussetzung. zeigen lässt, aus einer Voraussetzung.
Ansonsten hilft oft die "Schmierzettelmethode": Nimm auf einem Schmierzettel an, du hättest ein Element  , für das , für das  gilt. Folgere eine möglichst "aussagekräftige" Aussage gilt. Folgere eine möglichst "aussagekräftige" Aussage 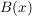 über über  , im Idealfall eine Aussage der Form " , im Idealfall eine Aussage der Form " ". Finde ein Beispiel für ein ". Finde ein Beispiel für ein  , für das , für das 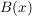 gilt. Wichtig: Ignoriere dann den Inhalt des Schmierzettels und beweise, dass das gefundene gilt. Wichtig: Ignoriere dann den Inhalt des Schmierzettels und beweise, dass das gefundene  die Aussage die Aussage  erfüllt. erfüllt.
Beispiele: Gruppe (Schmierzettelmethode), Surjektivität (Beispiel-Element aus Voraussetzungen)
h) Wie zeige ich die Gleichheit zweier Mengen?
Für eine Aussage der Form 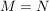 mit gewissen Mengen mit gewissen Mengen 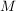 und und  zeige nacheinander zeige nacheinander  und und  wie unter i) beschrieben. wie unter i) beschrieben.
Beispiel: Gleichheit von Mengen
i) Wie zeige ich, dass eine Menge Teilmenge einer anderen Menge ist?
Für eine Aussage der Form  mit gewissen Mengen mit gewissen Mengen 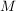 und und  betrachte ein beliebig vorgegebenes Element betrachte ein beliebig vorgegebenes Element  ("Sei ("Sei  .") und zeige unter der zusätzlichen Voraussetzung .") und zeige unter der zusätzlichen Voraussetzung  die Aussage die Aussage  . .
Da  beliebig vorgegeben war, gilt somit beliebig vorgegeben war, gilt somit  für alle für alle  ; also gilt ; also gilt  . .
Der Punkt i) ist eigentlich überflüssig, denn er ergibt sich aus der Definition von  als "für alle"-Aussage und dem unter f) beschriebenen Verfahren für solche Aussagen. Da jedoch sehr häufig Teilmengenbeziehungen zu zeigen sind, kann es nicht schaden, diese Anwendung von f) explizit zu kennen. als "für alle"-Aussage und dem unter f) beschriebenen Verfahren für solche Aussagen. Da jedoch sehr häufig Teilmengenbeziehungen zu zeigen sind, kann es nicht schaden, diese Anwendung von f) explizit zu kennen.
Beispiele: Teilmengenbeziehung 1, Teilmengenbeziehung 2, Gleichheit von Mengen
| 
